Integrate Sin 3x Cos 2x

Integral of Sin 3x

Integral of sin 3x is given by (-ane/iii) cos 3x + C. The integral of sin 3x is called the anti-derivative of sin 3x as integration is the reverse process differentiation. Sin 3x is an important trigonometric formula that is used to solve diverse bug in trigonometry. The integral of sin 3x can be calculated using the substitution method and using the sin 3x formula.

In this article, nosotros will summate the integral of sin 3x, bear witness it using the exchange method and sin 3x formula and make up one's mind the definite integral of sin 3x using different limits.

one.	What is Integral of Sin 3x?
2.	Integral of Sin 3x Formula
3.	Integral of Sin 3x Using Substitution Method
4.	Integral of Sin 3x Using Sin 3x Formula
5.	Definite Integral of Sin 3x
half-dozen.	FAQs on Integral of Sin 3x

What is Integral of Sin 3x?

The integral of sin 3x can be calculated using the formula for the integral of sin ax which is given past ∫sin (ax) dx = (-1/a) cos ax + C. Mathematically, the integral of sin 3x is written as ∫sin 3x dx = (-one/iii) cos 3x + C, where C is the abiding of integration, dx denotes that the integration of sin 3x is with respect to x, ∫ is the symbol for integration. The integral of sin 3x can also be evaluated using the substitution method and sin 3x formula.

Integral of Sin 3x Formula

Sin 3x formula is given by sin 3x = iii sin x - 4 sin^three10 and the formula for the integral of sin 3x is given by, ∫sin 3x dx = (-i/three) cos 3x + C, where C is the constant of integration.

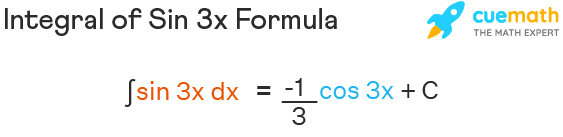
Integral of sin 3x

Integral of Sin 3x Using Substitution Method

At present, we know that the integral of sin 3x is (-1/3) cos 3x + C, where C is the constant of integration. Permit us prove this using the substitution method. Nosotros will utilise the following formulas of integration and differentiation:

∫sin x dx = -cos x + C
d(ax)/dx = a

Assume 3x = u, and then differentiating 3x = u with respect to 10, nosotros have 3dx = du ⇒ dx = (ane/three)du. Using the above formulas, nosotros have

∫sin 3x dx = ∫sin u (du/3)

⇒ ∫sin 3x dx = (i/3) ∫sin u du

⇒ ∫sin 3x dx = (1/3) (-cos u + C) [Considering ∫sin x dx = -cos x + C]

⇒ ∫sin 3x dx = (-1/3) cos u + C/3

⇒ ∫sin 3x dx = (-ane/iii) cos 3x + Grand, where K = C/3

Hence, we have derived the integral of sin 3x using the substitution method.

Integral of Sin 3x Using Sin 3x Formula

We know that the sin 3x formula is sin 3x = 3 sin 10 - four sin³x. Next, nosotros will prove that the integration of sin 3x is given by (-1/3) cos 3x + C using the sin 3x formula. Earlier proving the integral of sin 3x, we will derive the integral of sin cube x, that is, sin³ten. Nosotros will use the following formulas to prove the integral of sin³ten:

cos²x + sin²x = 1 ⇒ sin²x = one - cos²10
∫sin ten dx = -cos x dx

∫sin³10 dx = ∫sin x. sin²x dx

= ∫sin x.(1 - cosⁱⁱten) dx

= ∫sin x dx - ∫sin x. cos²ten dx --- (ane)

= I₁ - I_two, where I₁ = ∫sin x dx and I_two= ∫sin 10. cos²x dx

Now, I₁ = ∫sin 10 dx = -cos 10 + C₁, where C₁ is the constant of integration ---- (2)

For I₂= ∫sin x. cos²x dx, assume cos x = u ⇒ -sin 10 dx = du ⇒ sin x dx = -du

I₂= ∫sin x. cos^twoten dx

= ∫u² (-du)

= - ∫u² du

= - u³/iii + C_two, where C₂ is the abiding of integration

= (-i/3) cos³x + C₂---- (three)

Subsitute the values from (two) and (3) in (1),

∫sin^threeten dx = (-cos x + C₁) - ((-ane/three) cos³x + C₂)

= -cos x + (1/three) cos³x + C₁ - C_two

= -cos x + (1/3) cos³x + C, where C = C₁ - C_ii

⇒ ∫sin³ten dx = -cos x + (1/3) cos³x + C --- (iv)

Now that we have derived the integral of sin^threex, we will apply this formula along with some other formulas to derive the integral of sin 3x:

∫sin x dx = -cos x dx
∫sinⁱⁱⁱx dx = -cos x + (1/iii) cosⁱⁱⁱx + C
sin 3x = 3 sin 10 - 4 sin³x
cos 3x = 4cosⁱⁱⁱ10 - 3 cos x

Using the above formulas, nosotros have

∫sin 3x dx = ∫(3 sin x - 4 sin^threex) dx

= 3 ∫sin x dx - iv ∫sin³x dx

= 3(-cos x) - four(-cos x + (1/three) cosⁱⁱⁱx) + C, where C is the constant of integration

= -3 cos x + 4 cos x - (4/3)cosⁱⁱⁱten + C

= cos 10 - (4/iii)cos³ten + C

= (ane/iii)(3cos x - 4cosⁱⁱⁱten + 3C)

= (i/iii)(-cos 3x + 3C) [Because cos 3x = 4cos^three10 - 3 cos x]

= (-1/3) cos 3x + C

Hence, we accept derived the integration of sin 3x using the sin 3x formula.

Definite Integral of Sin 3x

We accept proved that the integral of sin 3x is (-1/three) cos 3x + C. Now, we volition determine the values of the definite integral of sin 3x with different limits. First, we will take the limits from 0 to π/iii.

Definite Integral of Sin 3x From 0 to π/3

\(\begin{align}\int_{0}^{\frac{\pi}{3}}\sin 3x \ dx &= \left [ -\frac{1}{3}\cos 3x+C \right ]_0^\frac{\pi}{3}\\&=\left ( -\frac{1}{3}\cos 3\frac{\pi}{iii}+C \right )-\left ( -\frac{1}{3}\cos three(0)+C\correct )\\&=-\frac{one}{3}\cos \pi+C + \frac{1}{3}\cos 0-C\\&= -\frac{1}{3}(-1)+\frac{1}{3}(1)\\&=\frac{2}{3}\end{align}\)

Hence the value of the definite integral of sin 3x with limits from 0 to π/3 is equal to 2/3.

Definite Integral of Sin 3x From 0 to Pi

\(\begin{align}\int_{0}^{\pi}\sin 3x \ dx &= \left [ -\frac{one}{3}\cos 3x+C \right ]_0^\pi\\&=\left ( -\frac{one}{3}\cos 3\pi+C \right )-\left ( -\frac{one}{three}\cos 3(0)+C\right )\\&=-\frac{1}{3}\cos 3\pi+C + \frac{1}{3}\cos 0-C\\&= -\frac{ane}{3}(-one)+\frac{ane}{iii}(1)\\&=\frac{two}{3}\end{align}\)

Hence the value of the definite integral of sin 3x with limits from 0 to π is equal to two/3.

Definite Integral of Sin 3x From 0 to Pi/2

\(\begin{marshal}\int_{0}^{\frac{\pi}{2}}\sin 3x \ dx &= \left [ -\frac{1}{3}\cos 3x+C \right ]_0^\frac{\pi}{2}\\&=\left ( -\frac{1}{3}\cos three\frac{\pi}{2}+C \right )-\left ( -\frac{ane}{3}\cos 3(0)+C\right )\\&=-\frac{1}{3}\cos \frac{3\pi}{2}+C + \frac{1}{3}\cos 0-C\\&= -\frac{1}{iii}(0)+\frac{1}{three}(1)\\&=\frac{1}{3}\end{marshal}\)

Hence the value of the definite integration of sin 3x with limits from 0 to π/2 is equal to 1/3.

Important Notes on Integral of Sin 3x

The easiest way to decide the integral of sin 3x is using the formula ∫sin (ax) dx = (-1/a) cos ax + C.
The integral of sin 3x is (-1/3) cos 3x + C and the integral of sin cube x is ∫sin³ten dx -cos x + (ane/3) cos³x + C.

Related Topics

Integral of Tan 2x
Cos 3x
Sin 3x

Integral of Sin 3x Examples

Instance one: Determine the integral of sin 3x cosec 3x.

Solution: Nosotros know that sin x =one/cosec ten and cosec 10 = ane/sin 10, and then we have

∫sin 3x cosec 3x dx = ∫sin (1/sin 3x) dx

= ∫1dx

= x + C

Answer: Hence the integral of sin 3x cosec 3x is 10 + C.
Instance ii: Evaluate the integral of sin 3x e^{cos 3x}.

Solution: To evaluate the integral of sin 3x e^{cos 3x}, nosotros will assume cos 3x = u.

Differentiating cos 3x = u with respect x, we get

-iii sin 3x dx = du

⇒ sin 3x = (-1/3) du

We accept,

∫sin 3x east^{cos 3x}dx = ∫(-1/three)eastward^u du

= (-1/3) ∫e^u du

= (-1/iii) eastward^u + C

= (-ane/3) east^{cos 3x} + C

Answer: Hence, the integral of sin 3x e^{cos 3x} is (-i/3) east^{cos 3x} + C.

go to slidego to slide

Accept questions on basic mathematical concepts?

Get a trouble-solving champ using logic, not rules. Learn the why backside math with our certified experts

Book a Free Trial Class

Integral of Sin 3x Questions

get to slidego to slide

FAQs on Integral of Sin 3x

What is Integral of Sin 3x in Trigonometry?

In trigonometry, the integral of sin 3x is written every bit ∫sin 3x dx = (-1/iii) cos 3x + C, where C is the constant of integration.

How to Discover the Integral of Sin 3x?

The integral of sin 3x tin can be calculated using the formula for the integral of sin ax which is given by ∫sin (ax) dx = (-one/a) cos ax + C. It can also exist calculated using the commutation method and sin 3x formula.

What is the Definite Integral of Sin 3x from 0 to pi?

The value of the definite integral of sin 3x with limits from 0 to π is equal to ii/3.

What is the Integration of Sin³ten?

The integral of sin cube x is given by ∫sinⁱⁱⁱx dx = -cos x + (ane/iii) cos³x + C.

What is the Integral of Sin 2x?

The integral of sin 2x dx is written as ∫ sin 2x dx = -(cos 2x)/two + C, where C is the integration constant.